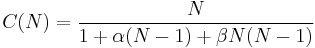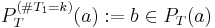Neil J. Gunther
| Neil James Gunther | |
|---|---|
Neil Gunther at Bletchley Park 2002
"A quantum leap is neither" |
|
| Born | August 15, 1950 Preston, Victoria, Australia |
| Residence | United States, California, |
| Nationality | Australia |
| Fields | Computational information systems (classical and quantum) |
| Institutions | San Jose State University Syncal Corporation Xerox Palo Alto Research Center Performance Dynamics Company (Founder) École Polytechnique Fédérale de Lausanne (EPFL) |
| Alma mater | La Trobe University University of Southampton |
| Doctoral advisor | Tomas M. Kalotas (Honors) Christie J. Eliezer (Masters) David J. Wallace (Doctorate) |
| Known for | Performance analysis Capacity planning tools Theory of large transients Universal scalability law |
Neil Gunther, (born 15 August 1950) is a computer information systems researcher best known internationally for developing the open-source performance modeling software Pretty Damn Quick and developing the Guerrilla approach to computer capacity planning and performance analysis. He has also been cited for his contributions to the theory of large transients in computer systems and packet networks, and his universal law of computational scalability.[1][2][3][4][5][6]
Gunther is a Senior Member of both the Association for Computing Machinery (ACM) and the Institute of Electrical and Electronics Engineers (IEEE), as well as a member of the American Mathematical Society (AMS), American Physical Society (APS), Computer Measurement Group (CMG) and ACM SIGMETRICS.
He is currently focused on developing quantum information system technologies.[7]
Contents |
Biography
Gunther is an Australian of German and Scots ancestry, born in Melbourne on 15 August 1950. He attended Preston East Primary School from 1955 to 1956, and Balwyn North Primary School from 1956 until 1962. For his tenth birthday, Gunther received a copy of the now famous book entitled The Golden Book of Chemistry Experiments from an older cousin. Inspired by the book, he started working on various experiments, making use of various chemicals that could be found around in his house. After he spilled some potassium permanganate solution on his bedroom carpet his mother confined him to an alcove in the garage which he turned into a small laboratory, replete with industrial chemicals and second-hand laboratory glassware. Gunther was interested in finding out how things like detergents and oils were composed by cracking them in his fractionating column. He took particular interest in mixing paints for his art classes, as well as his chemistry classes in Balwyn High School. His father, being the Superintendent of Melbourne's electrical power station, borrowed an organic chemistry text from the chemists in the quality control laboratory. This ultimately led to an intense interest in synthesizing Azo dyes. At around age 14, Gunther attempted to predict the color of azo dyes based on the chromophore-auxochrome combination. Apart from drawing up empirical tables, this effort was largely unsuccessful due to his lack of knowledge of quantum theory.
Post-Doc years
Gunther taught physics at San Jose State University from 1980-1981. He then joined Syncal Corporation, a small company contracted by NASA and JPL to develop thermoelectric materials for their deep-space missions. Gunther was asked to analyze the thermal stability test data from the Voyager RTGs. He discovered that the stability of the silicon-germanium (Si-Ge) thermoelectric alloy was controlled by a soliton-based precipitation mechanism.[8] JPL used his work to select the next generation of RTG materials for the Galileo mission launched in 1989.
Xerox years
In 1982, Gunther joined Xerox PARC to develop parametric and functional test software for PARC's small-scale VLSI design fabrication line. Ultimately, he was recruited onto the Dragon multiprocessor workstation project where he also developed the PARCbench multiprocessor benchmark. This was his first fore into computer performance analysis.
1989, he developed a Wick-rotated version of Richard Feynman's quantum path integral formalism for analyzing performance degradation in large-scale computer systems and packet networks.[9]
Pyramid years
In 1990 Gunther joined Pyramid Technology (now part of Fujitsu Siemens Computers) where he held positions as Senior Scientist and Manager of the Performance Analysis Group that was responsible for attaining industry-high TPC benchmarks on their Unix multiprocessors. He also performed simulations for the design of the Reliant RM1000 parallel database server.
Consulting practice
Gunther founded Performance Dynamics Company as a sole proprietorship, registered in California in 1994, to provide consulting and educational services for the management of high performance computer systems with an emphasis on performance analysis and enterprise-wide capacity planning. He went on to release and develop his own open-source performance modeling software called "PDQ (Pretty Damn Quick)" around 1998. That software also accompanied his first textbook on performance analysis entitled The Practical Performance Analyst. Several other books have followed since then.
Current research interests
Quantum information systems
In 2004, Gunther has embarked on joint research into quantum information systems based on photonics.[7] During the course of his research in this area, he has developed a theory of photon bifurcation that is currently being tested experimentally at École Polytechnique Fédérale de Lausanne.[10] This represents yet another application of path integral formulation to circumvent the wave-particle duality of light.
In its simplest rendition, this theory can be considered as providing the quantum corrections to the Abbe-Rayleigh diffraction theory of imaging and the Fourier theory of optical information processing.[11]
Performance visualization
Inspired by the work of Tukey, Gunther explored ways to help systems analyst visualize performance in a manner similar to that already available in scientific visualization and information visualization. In 1991, he developed a tool called Barry, which employs barycentric coordinates to visualize sampled CPU usage data on large-scale multiprocessor systems.[12] More recently, he has applied the same 2-simplex barycentric coordinates to visualizing the Apdex application performance metric, which is based on categorical response time data. A barycentric 3-simplex] (a tetrahedron), that can be swivelled on the computer screen using a mouse, has been found useful for visualizing packet network performance data. In 2008, he co-founded the PerfViz google group.
Universal Law of Computational Scalability
The relative capacity C(N) of a computational platform is given by:
where N represents either the number of physical processors in the hardware configuration or the number of users driving the software application. The parameters  and
and  represent respectively the levels of contention (e.g., queueing for shared resources) and coherency delay (i.e., latency for data to become consistent) in the system. The
represent respectively the levels of contention (e.g., queueing for shared resources) and coherency delay (i.e., latency for data to become consistent) in the system. The  parameter also quantifies the retrograde throughput seen in many stress tests but not accounted for in either Amdahl's law or event-based simulations. This scalability law was originally developed by Gunther in 1993 while he was employed at Pyramid Technology.[13] Since there are no topological dependencies, C(N) can model symmetric multiprocessors, multicores, clusters, and GRID architectures. Also, because each of the three terms has a definite physical meaning, they can be employed as a heuristic to determine where to make performance improvements in hardware platforms or software applications.
parameter also quantifies the retrograde throughput seen in many stress tests but not accounted for in either Amdahl's law or event-based simulations. This scalability law was originally developed by Gunther in 1993 while he was employed at Pyramid Technology.[13] Since there are no topological dependencies, C(N) can model symmetric multiprocessors, multicores, clusters, and GRID architectures. Also, because each of the three terms has a definite physical meaning, they can be employed as a heuristic to determine where to make performance improvements in hardware platforms or software applications.
At a more fundamental level, the above equation can be derived[14] from the Machine Repairman queueing model:[15]
Theorem (Gunther 2008): The universal scalability law is equivalent to the synchronous queueing bound on throughput in a modified Machine Repairman with state-dependent service times.
The following corollary (Gunther 2008 with 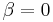 ) corresponds to Amdahl's law:[16]
) corresponds to Amdahl's law:[16]
Theorem (Gunther 2002): Amdahl's law for parallel speedup is equivalent to the synchronous queueing bound on throughput in a Machine Repairman model of a multiprocessor.
Computational mathematics
Over the past fifteen years, Gunther has had an abiding interest in of the 3x+1 problem, not with the goal of developing a technical proof of the original conjecture but rather, using computers as a tool to examine it for structure that might lead to better computer-generated visualizations of this and related problems in number theory. In one early attempt along these lines he employed VRML.[17] Paul Erdös famously stated about the 3x+1 problem, "Mathematics is not yet ready for such problems." Gunther thinks that perhaps computers are.
More formally, Gunther has developed a functional Diophantine equation that generalizes Terra’s theorem (1976) and is based on a graphical primitive: the G-set. The G-set is related to the predecessor sets of Wirsching by the following theorem.[18]
Theorem (Gunther 1999): The G-set (
) is a directed subgraph in
(Collatz tree) formed by acyclic predecessor sets starting at b and terminating at vertex a with exactly k = 1 edges arising from
, i.e.,
.
The proof is unpublished. This theorem leads to the following conjecture for the construction of 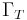 .
.
Conjecture (Gunther 1999):
, where
, enumerates all G-cells in
such that the unique G-set
contains the degenerate cycle
.
Ironically, given his lack of intent to find a proof, the formal associations with the theorems of Terras and Wirsching, make it plausible that this method of sub-graph enumeration might form the basis of an inductive proof.
Awards
- Senior Member ACM (elected April 2009).
- Senior Member IEEE (elected February 2009).
- Recipient of the A. A. Michelson Award, December 2008.
- Summer Research Institute visitor, EPFL 2006 and 2007.
- Lecturer, Western Institute of Computer Science, Stanford University, 1997-2000.
- Best paper award, CMG conference 1996.
- Visiting Scholar in Materials Science, Stanford University, 1981-1982.
- Science Research Council Studentship, U.K. 1976-1980.
- Commonwealth Postgraduate Scholarship, Australia 1975-1976.
Quotes
- As a consultant, I offer more harangue for the buck.
- Lately, I've been solicited to give so many talks I feel like Mister Ed The Talking Whore.
- It's better to have wrong expectations, than no expectations.[19]
- Best Practices are an admission of failure.[19]
- A queue is a line of customers waiting to be severed.
- The only dumb question is the one never asked.
- A quantum leap is neither.
- Art irritates life.[20]
- If you want to be more productive, go to sleep.
- All meaning has a pattern, but not all patterns have a meaning.
Selected bibliography
Theses
- The Feynman Path Integral in Non-Relativistic Quantum Mechanics and Quantum Electrodynamics, La Trobe University (AUS),
B.Sc. Honors dissertation, Department of Physics, Oct. (1974)
- Dynamical Symmetry Groups: The Study and Interpretation of Certain Invariants as Group Generators in Quantum Mechanics, La Trobe
University (AUS), M.Sc. dissertation, Department of Applied Mathematics, Nov. (1976)
- Broken Dynamical Symmetries in Quantum Field Theory and Phase Transition Phenomena, University of Southampton (U.K.), Ph.D.
dissertation, Department of Physics, Dec. (1979)
Books
- The Practical Performance Analyst, McGraw-Hill, New York, New York 1998, ISBN 0079129463 (Out of print)
- The Practical Performance Analyst, iUniverse.com Press, Lincoln, Nebraska 2000, ISBN 059512674X (Reprint edition)
- Performance Engineering: State of the Art and Current Trends, Lecture Notes in Computer Science, Springer-Verlag
Heidelberg, Germany, October 2001, ISBN 3540421459 (Contributed chapter)
- Analyzing Computer System Performance with Perl::PDQ, Springer, Heidelberg 2005, ISBN 3540208658
- Guerrilla Capacity Planning, Springer, Heidelberg 2007, ISBN 3540261389
Invited presentations
- Goldstone Modes in First-order Phase Transitions, Sixth West Coast Conference on Statistical Mechanics, IBM Research Laboratories, San Jose, June (1980)
- Instanton Techniques for Queueing Models of Large Computer Systems: Getting a Piece of the Action, SIAM Conference on Applied Probability in Science and Engineering, New Orleans, Louisiana, March (1990)
- (Numerical) Investigations into Physical Power-law Models of Internet Traffic Using the Renormalization Group, IFORS Conference of Operations Research Societies, Honolulu, Hawaii, July 11–15 (2005)
Papers
- Goldstone Modes in Vacuum Decay and First-order Phase Transitions, Journal of Physics, A, 13, 1755-1767 (1980)
- A Benchmark for Image Retrieval using Distributed Systems over the Internet (2000 with G. Beretta)
- Performance and Scalability Models for a Hypergrowth e-Commerce Web Site (2000)
- Characterization of the Burst Stabilization Protocol for the RR/CICQ Switch (2003 with K. J. Christensen and K. Yoshigoe)
- Unification of Amdahl's Law, LogP and Other Performance Models for Message-Passing Architectures (2005)
- Towards Practical Design Rules for Quantum Communications and Quantum Imaging Devices (2005 with G. Beretta)
- The Virtualization Spectrum from Hyperthreads to GRIDs, Proc. CMG Conf., Reno, Nevada, Dec. (2006)
References
- ^ Microsoft developer blog comparing Amdahl's law with Gunther's law (2009)
- ^ Computer Measurement Group Interview part 1 and part 2 (2009)
- ^ Springer author biography
- ^ Oracle performance experts
- ^ La Trobe University alumnus profile
- ^ Interview with John C. Dvorak (1998)
- ^ a b D. L. Boiko, Neil J. Gunther, N. Brauer, M. Sergio, C. Niclass, G. Beretta. and E. Charbon (2009). "A Quantum Imager for Intensity Correlated Photons". New Journal of Physics. http://www.iop.org/EJ/journal/-page=forthart/1367-2630.
- ^ Gunther, Neil J. (1982). ""Solitons and Their Role in the Degradation of Modified Silicon-Germanium Alloys" in Proc. IEEE Fourth Int. Conf. on Thermoelectric Energy Conversion.". IEEE, Volume 82CH1763-2, Pages 89–95. http://www.neilgunther.com/DeepSpace/thermo82.pdf.
- ^ Gunther, Neil J. (1989). "Path Integral Methods for Computer Performance Analysis". Information Processing Letters, Volume 32(1) Pages 7–13. http://dblp.uni-trier.de/rec/bibtex/journals/ipl/Gunther89.
- ^ Gunther, Neil J. , E. Charbon, D. L. Boiko, and G. Beretta (2006). "Photonic Information Processing Needs Quantum Design Rules". SPIE Online. http://spie.org/x8567.xml?pf=true&highlight=x2410.
- ^ E. G. Steward (2004). Fourier Optics: An Introduction. Dover. ISBN 0-486-43504-0.
- ^ Gunther, Neil J. (1992). "On the Application of Barycentric Coordinates to the Prompt and Visually Efficient Display of Multiprocessor Performance Data" in Proc. VI International Conf. on Modelling Techniques and Tools for Computer Performance Evaluation, Edinburgh, Scotland. Antony Rowe Ltd., Wiltshire, U.K., Pages 67–80. ISBN 0-7486-0425-1.
- ^ Gunther, Neil J. (1993). ""A Simple Capacity Model for Massively Parallel Transaction Systems" in Proc. CMG Conf., San Diego, California". CMG, Pages 1035–1044. http://www.perfdynamics.com/Papers/njgCMG93.pdf.
- ^ Neil J. Gunther (2008). "A General Theory of Computational Scalability Based on Rational Functions". arXiv:0808.1431v2 [cs.PF].
- ^ D. Gross and C. M. Harris (1998). Fundamentals of Queueing Theory. Wiley-Interscience. ISBN 0-471-17083-6.
- ^ Gunther, Neil J. (2002). "A New Interpretation of Amdahl's Law and Geometric Scalability". arXiv:cs/0210017 [cs.DC].
- ^ Gunther, Neil J. (2000). ""Seeing the Forest in the Tree: Applying VRML to Mathematical Problems in Number Theory" in Proc. IEEE-SPIE 12th International Symposium on Internet Imaging". Proc. IEEE-SPIE th International Symposium on Internet Imaging (SPIE International Society for Optical Engineering, Volume 3964) 2000 (12). arXiv:cs/9912021. Bibcode 1999SPIE.3964..214G.
- ^ Wirsching, Günther J. (1998). The Dynamical System Generated by the 3n+1 Function. Springer Lecture Notes in Mathematics, Number 1681. ISBN 3-540-63970-5.
- ^ a b Guerrilla Manifesto
- ^ Perversion of a quote from Oscar Wilde.
External links
- Performance Dynamics Company(SM)
- Performance blog
- The Mathematics Genealogy Project
- OEIS Binary Carry Sequence: Mathematica code (May 23 2009)
- M.Sc. Thesis at National Library of Australia
- List of papers on arXiv
- List of papers on computer performance analysis
- Dirac Number 2
- Guerrilla Manifesto
- PDQ performance modeling software
- Performance Visualization
- Linked-in profile